 The intent of this article is not to tell you everything you wanted to know about artificial neural networks (ANN) and were afraid to ask. For that you’ll have to ask someone else. Here I only intend to tell you how you might use R to implement an ANN model. One thing I will say is that I rarely use an ANN. I have found them to work best in an ensemble model (using averaging) with logistics regression models.
The intent of this article is not to tell you everything you wanted to know about artificial neural networks (ANN) and were afraid to ask. For that you’ll have to ask someone else. Here I only intend to tell you how you might use R to implement an ANN model. One thing I will say is that I rarely use an ANN. I have found them to work best in an ensemble model (using averaging) with logistics regression models.
Using neuralnet
neuralnet depends on two other packages: grid and MASS (Venables and Ripley, 2002). It is used is primarily with functions dealing with regression analyses like linear models (lm) and general linear models (glm). As essential arguments, we must specify a formula in terms of response variables ~ sum of covariates and a data set containing covariates and response variables. Default values are defined for all other parameters (see next subsection). We use the data set infert that is provided by the package datasets to illustrate its application. This data set contains data of a case-control study that investigated infertility after spontaneous and induced abortion (Trichopoulos et al., 1976). The data set consists of 248 observations, 83 women, who were infertile (cases), and 165 women, who were not infertile (controls). It includes amongst others the variables age, parity, induced, and spontaneous. The variables induced and spontaneous denote the number of prior induced and spontaneous abortions, respectively. Both variables take possible values 0, 1, and 2 relating to 0, 1, and 2 or more prior abortions. The age in years is given by the variable age and the number of births by parity.
Training of neural networks
The function neuralnet, used for training a neural network, provides the opportunity to define the required number of hidden layers and hidden neurons according to the needed complexity. The complexity of the calculated function increases with the addition of hidden layers or hidden neurons. The default value is one hidden layer with one hidden neuron. The most important arguments of the function are the following:
- formula, a symbolic description of the model to be fitted (see above). No default.
- data, a data frame containing the variables specified in formula. No default.
- hidden, a vector specifying the number of hidden layers and hidden neurons in each layer. For example the vector (3,2,1) induces a neural network with three hidden layers, the first
- startweights, a vector containing prespecified starting values for the weights. Default: random numbers drawn from the standard normal distribution
- algorithm, a string containing the algorithm type. Possible values are “backprop“, “rprop+”, “rprop-“, “sag“, or “slr“. “backprop” refers to traditional backpropagation, “rprop+” and “rprop-” refer to resilient backpropagation with and without weight backtracking and “sag” and “slr” refer to the modified globally convergent algorithm (gr-prop). “sag” and “slr” define the learning rate that is changed according to all others. “sag” refers to the smallest absolute derivative, “slr” to the smallest learning rate. Default: “rprop+”
- err.fct, a differentiable error function. The strings “sse” and “ce” can be used, which refer to ‘sum of squared errors’ and ‘cross entropy’. Default: “sse“
- act.fct, a differentiable activation function. The strings “logistic” and “tanh” are possible for the logistic function and tangens hyperbolicus (that is the Latin name for hyperbolic tangent). Default: “logistic“
- linear.output, logical. If act.fct should not be applied to the output neurons, linear.output has to be TRUE. Default: TRUE
- likelihood, logical. If the error function is equal to the negative log-likelihood function, likelihood has to be TRUE. Akaike’s Information Criterion (AIC, Akaike, 1973) and Bayes Information Criterion (BIC, Schwarz, 1978) will then be calculated. Default: FALSE
- exclude, a vector or matrix specifying weights that should be excluded from training. A matrix with n rows and three columns will exclude n weights, where the first column indicates the layer, the second column the input neuron of the weight, and the third neuron the output neuron of the weight. If given as vector, the exact numbering has to be known. The numbering can be checked using the provided plot or the saved starting weights. Default: NULL
- constant.weights, a vector specifying the values of weights that are excluded from training and treated as fixed. Default: NULL
The usage of neuralnet is described by modeling the relationship between the case-control status (case) as response variable and the four covariates age, parity, induced and spontaneous. Since the response variable is binary, we could chose the logistic function (default) as the activation function and (err.fct=”ce”) as the error function as cross-entropy. Additionally, we should state the item linear.output as FALSE to ensure that the output is mapped by the activation function to the interval [0, 1]. The number of hidden neurons should be determined in relation to the needed complexity. A neural network with, for example, two hidden neurons is trained by the following statements:
> library(neuralnet)
Loading required package: grid
Loading required package: MASS
> nn nn
Call:
neuralnet(formula = case~age+parity+induced+spontaneous, data = infert, hidden = 2, err.fct = "ce", linear.output = FALSE)
1 repetition was calculated.
Error Reached Threshold Steps
1 125.2126851 0.008779243419 5254
We save basic information about the training process and the trained neural network in nn. This includes all information that has to be known to reproduce the results as for instance the starting weights. Important values are the following:
- net.result, a list containing the overall result, i.e. the output, of the neural network for each replication.
- weights, a list containing the fitted weights of the neural network for each replication.
- generalized.weights, a list containing the generalized weights of the neural network for each replication.
- result.matrix, a matrix containing the error, reached threshold, needed steps, AIC and BIC (computed if likelihood=TRUE) and estimated weights for each replication. Each column represents one replication.
- startweights, a list containing the starting weights for each replication.
A summary of the main results is provided by nn$result.matrix:
> nn$result.matrix
1 error 125.212685099732
reached.threshold 0.008779243419
steps 5254.000000000000
Intercept.to.1layhid1 5.593787533788
age.to.1layhid1 -0.117576380283
parity.to.1layhid1 1.765945780047
induced.to.1layhid1 -2.200113693672
spontaneous.to.1layhid1 -3.369491912508
Intercept.to.1layhid2 1.060701883258
age.to.1layhid2 2.925601414213
parity.to.1layhid2 0.259809664488
induced.to.1layhid2 -0.120043540527
spontaneous.to.1layhid2 -0.033475146593
Intercept.to.case 0.722297491596
1layhid.1.to.case -5.141324077052
1layhid.2.to.case 2.623245311046
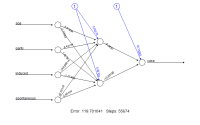
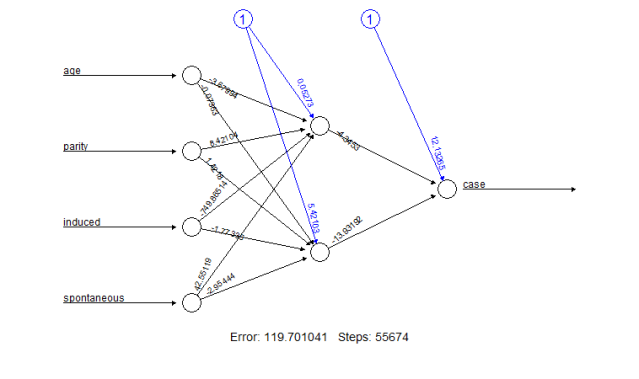
The training process needed 5254 steps until all absolute partial derivatives of the error function were smaller than 0.01 (the default threshold). The estimated weights range from −5.14 to 5.59. For instance, the intercepts of the first hidden layer are 5.59 and 1.06 and the four weights leading to the first hidden neuron are estimated as −0.12, 1.77, −2.20, and −3.37 for the covariates age, parity, induced and spontaneous, respectively. If the error function is equal to the negative log-likelihood function, the error refers to the likelihood as is used for example to calculate Akaike’s Information Criterion (AIC).
We save the given data in nn$covariate and nn$response as well as in nn$data for the whole data set inclusive non-used variables. The output of the neural network, i.e. the fitted values o(x), is provided by nn$net.result:
> out
> dimnames(out) head(out)
Age parity induced spontaneous nn-output
[1,] 26 6 1 2 0.1519579877
[[2,] 42 1 1 0 0.6204480608
[[3,] 39 6 2 0 0.1428325816
[[4,] 34 4 2 0 0.1513351888
[[5,] 35 3 1 1 0.3516163154
[[6,] 36 4 2 1 0.4904344475
In this case, the object nn$net.result is a list consisting of only one element relating to one calculated replication. If more than one replication were calculated, we would save the each of the outputs in a separate list element. This approach is the same for all values that change with replication apart from net.result that is saved as matrix with one column for each replication.
To compare the results, neural networks are trained with the same parameter setting as above using neuralnet with algorithm=”backprop” and the package nnet.
> nn.bp nn.bp
Call:
neuralnet(formula = case~age+parity+induced+spontaneous, data = infert, hidden = 2, learningrate = 0.01, algorithm = "backprop", err.fct = "ce", linear.output = FALSE)
1 repetition was calculated.
Error Reached Threshold Steps
1 158.085556 0.008087314995 4
> nn.nnet # weights: 13
initial value 256.848809
iter 10 value 158.085559
final value 158.085463
converged
nn.bp and nn.nnet show equal results. Both training processes last only a very few iteration steps and the error is approximately 158. Thus, in this little comparison, the model fit is less satisfying than that achieved by resilient backpropagation.
neuralnet includes the calculation of generalized weights as introduced by Intrator and Intrator (2001). The generalized weight w̃i is defined as the contribution of the ith covariate to the log-odds:
The generalized weight expresses the effect of each covariate xi and thus has an analogous interpretation as the ith regression parameter in regression models. However, the generalized weight depends on all other covariates. Its distribution indicates whether the effect of the covariate is linear since a small variance suggests a linear effect (Intrator and Intrator, 2001). They are saved in nn$generalized.weights and are given in the following format (rounded values)
> head(nn$generalized.weights[[1]])
[,1] [,2] [,3] [,4]
1 0.0088556 -0.1330079 0.1657087 0.2537842
2 0.1492874 -2.2422321 2.7934978 4.2782645
3 0.0004489 -0.0067430 0.0084008 0.0128660
4 0.0083028 -0.1247051 0.1553646 0.2379421
5 0.1071413 -1.6092161 2.0048511 3.0704457
6 0.1360035 -2.0427123 2.5449249 3.8975730
The columns refer to the four covariates age (j =1), parity (j = 2), induced (j = 3), and spontaneous(j = 4) and a generalized weight is given for each observation even though they are equal for each covariate combination.
Visualizing the results
The results of the training process can be visualized by two different plots. First, the trained neural network can simply be plotted by
> plot(nn)
The resulting plot is given in Figure 1.
Figure 1: Plot of a trained neural network including trained synaptic weights and basic information about the training process.
It reflects the structure of the trained neural network, i.e. the network topology. The plot includes by default the trained synaptic weights, all intercepts as well as basic information about the training process like the overall error and the number of steps needed to converge. Especially for larger neural networks, the size of the plot and that of each neuron can be determined using the parameters dimension and radius, respectively.
The second possibility to visualize the results is to plot generalized weights. gwplot uses the calculated generalized weights provided by nn$generalized.weights and can be used by the following statements:
> par(mfrow=c(2,2))
> gwplot(nn, selected.covariate="age", min=-2.5, max=5)
> gwplot(nn, selected.covariate="parity",
+ min=-2.5, max=5)
> gwplot(nn, selected.covariate="induced",
+ min=-2.5, max=5)
> gwplot(nn, selected.covariate="spontaneous",
+ min=-2.5, max=5)
The corresponding plot is shown in Figure 2.
Figure 2: Plots of generalized weights with respect to each covariate.
The generalized weights are given for all covariates within the same range. The distribution of the generalized weights suggests that the covariate age has no effect on the case-control status since all generalized weights are nearly zero and that at least the two covariates induced and spontaneous have a non-linear effect since the variance of their generalized weights is overall greater than one.
Additional features
The compute function
compute calculates and summarizes the output of each neuron, i.e. all neurons in the input, hidden and output layer. Thus, it can be used to trace all signals passing the neural network for given covariate combinations. This helps to interpret the network topology of a trained neural network. It can also easily be used to calculate predictions for new covariate combinations. A neural network is trained with a training data set consisting of known input-output pairs. It learns an approximation of the relationship between inputs and outputs and can then be used to predict outputs o(xnew ) relating to new covariate combinations xnew . The function compute simplifies this calculation. It automatically redefines the structure of the given neural network and calculates the output for arbitrary covariate combinations.
To stay with the example, predicted outputs can be calculated for instance for missing combinations with age=22, parity=1, induced ≤ 1, and spontaneous ≤ 1. They are provided by new.output$net.result
> new.output new.output$net.result
[,1]
[1,] 0.1477097
[2,] 0.1929026
[3,] 0.3139651
[4,] 0.8516760
This means that the predicted probability of being a case given the mentioned covariate combinations, i.e. o(x), is increasing in this example with the number of prior abortions.
The confidence.interval function
The weights of a neural network follow a multivariate normal distribution if the network is identified (White, 1989). A neural network is identified if it does not include irrelevant neurons, neither in the input layer nor in the hidden layers. An irrelevant neuron in the input layer can be, for instance, a covariate that has no effect or that is a linear combination of other included covariates. If this restriction is fulfilled and if the error function equals the negative log-likelihood, a confidence interval can be calculated for each weight. The neuralnet package provides a function to calculate these confidence intervals regardless of whether all restrictions are fulfilled. Therefore, we have to be careful interpreting the results.
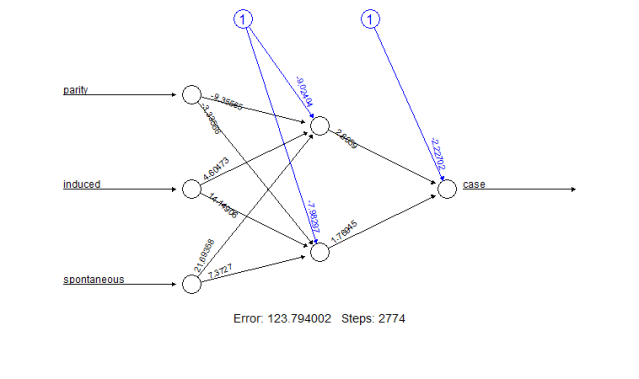
Since the covariate age has no effect on the outcome and the related neuron is thus irrelevant, a new neural network (nn.new), which has only the three input variables parity, induced, and spontaneous, has to be trained to demonstrate the usage of confidence.interval. Let us assume that all restrictions are now fulfilled, i.e. neither the three input variables nor the two hidden neurons are irrelevant. Confidence intervals can then be calculated with the function confidence.interval:
> nn.new nn.new
Call: neuralnet(formula = case ~ parity + induced + spontaneous, data = infert, hidden = 2, err.fct = "ce", linear.output = FALSE)
1 repetition was calculated.
Error Reached Threshold Steps
1 123.7940021 0.009743898478 2774
> nn.new$result.matrix
1
error 123.794002097050
reached.threshold 0.009743898478
steps 2774.000000000000
Intercept.to.1layhid1 -9.024035981211
parity.to.1layhid1 -9.355649895691
induced.to.1layhid1 4.604728544071
spontaneous.to.1layhid1 21.693583835740
Intercept.to.1layhid2 -7.982974207707
parity.to.1layhid2 -3.335661191123
induced.to.1layhid2 14.149057774749
spontaneous.to.1layhid2 7.372698725819
Intercept.to.case -2.227015901571
1layhid.1.to.case 2.805901061643
1layhid.2.to.case 1.769454351740
> out dimnames(out) head(out)
parity induced spontaneous nn.new-output
[1,] 6 1 2 0.2748949333
[2,] 1 1 0 0.3644454394
[3,] 6 2 0 0.2296907484
[4,] 4 2 0 0.3871712281
[5,] 3 1 1 0.3757109614
[6,] 4 2 1 0.3875643222
> head(nn.new$generalized.weights[[1]])
[,1] [,2] [,3]
1 -1.214196782891496 5.15032191028160 2.68369804196508
2 -0.310485049736654 1.31689903088964 0.68625753443013
3 -1.442613638423590 6.11921371721348 3.18855996591000
4 -0.005521928145309 0.02342266671564 0.01220493037762
5 -0.163520412577241 0.69159093349938 0.36148214704463
6 -0.000008138035933 0.00001703598866 0.00001849315091
> plot(nn.new)
> new.output new.output$net.result
[,1]
[1,] 0.09735243992
[2,] 0.36444543943
[3,] 0.91271565323
> ci ci$lower.ci
[[1]]
[[1]][[1]]
[,1] [,2]
[1,] -18.323535695 -18.920799122
[2,] -17.278014756 -9.526947243
[3,] 1.659472408 -9.344351919
[4,] 2.390600705 -4.210395184
[[1]][[2]]
[,1]
[1,] -2.9311558742
[2,] 1.8202683312
[3,] 0.9017336937
Figure 3: Plot of the new trained neural network including trained synaptic weights and basic information about the training process.
For each weight, ci$lower.ci provides the related lower confidence limit and ci$upper.ci the related upper confidence limit. The first matrix contains the limits of the weights leading to the hidden neurons. The columns refer to the two hidden neurons. The other three values are the limits of the weights leading to the output neuron.
Summary
This paper gave a brief introduction to multilayer perceptrons and supervised learning algorithms. It introduced the package neuralnet that can be applied when modeling functional relationships between covariates and response variables. neuralnet contains a very flexible function that trains multilayer perceptrons to a given data set in the context of regression analyses. It is a very flexible package since most parameters can be easily adapted. For example, the activation function and the error function can be arbitrarily chosen and can be defined by the usual definition of functions in R.
Bibliography
- Akaike. Information theory and an extension of the maximum likelihood principle. In Petrov BN and Csaki BF, editors, Second international symposium on information theory, pages 267–281. Academiai Kiado, Budapest, 1973.
- Almeida, C. Baugh, C. Lacey, C. Frenk, G. Granato, L. Silva, and A. Bressan. Modeling the dsty universe i: Introducing the artificial neural network and first applications to luminosity and color distributions. Monthly Notices of the Royal Astronomical Society, 402:544–564, 2010.
- Anastasiadis, G. Magoulas, and M. Vrahatis. New globally convergent training scheme based on the resilient propagation algorithm. Neurocomputing, 64:253–270, 2005.
- Bishop. Neural networks for pattern recognition. Oxford University Press, New York, 1995.
- Fritsch and F. Günther. neuralnet: Training of Neural Networks. R Foundation for Statistical Computing, 2008. R package version 1.2.
- Günther, N. Wawro, and K. Bammann. Neural networks for modeling gene-gene interactions in association studies. BMC Genetics, 10:87, 2009. http://www.biomedcentral.com/1471-2156/10/87.
- Hornik, M. Stichcombe, and H. White. Multilayer feedforward networks are universal approximators. Neural Networks, 2:359–366, 1989.
- Intrator and N. Intrator. Interpreting neural-network results: a simulation study. Computational Statistics & Data Analysis, 37:373–393, 2001.
- Kumar and D. Zhang. Personal recognition using hand shape and texture. IEEE Transactions on Image Processing, 15:2454–2461, 2006.
- C. Limas, E. P. V. G. Joaquín B. Ordieres Meré, F. J. M. de Pisón Ascacibar, A. V. P. Espinoza, and F. A. Elías. AMORE: A MORE Flexible Neural Network Package, 2007. URL http://wiki.r-project. org/rwiki/doku.php?id=packages:cran:amore. R package version 0.2-11.
- McCullagh and J. Nelder. Generalized Linear Models. Chapman and Hall, London, 1983.
- Riedmiller. Advanced supervised learning in multilayer perceptrons – from backpropagation to adaptive learning algorithms. International Journal of Computer Standards and Interfaces, 16:265–278,1994.
- Riedmiller and H. Braun. A direct method for faster backpropagation learning: the rprop algorithm. Proceedings of the IEEE International Conference on Neural Networks (ICNN), 1:586–591, 1993.
- Rocha, P. Cortez, and J. Neves. Evolutionary neu- ral network learning. Lecture Notes in Computer Science, 2902:24–28, 2003.
- Rojas. Neural Networks. Springer-Verlag, Berlin, 1996.
- Schiffmann, M. Joost, and R. Werner. Optimization of the backpropagation algorithm for training multilayer perceptrons. Technical report, University of Koblenz, Insitute of Physics, 1994.
- Schwarz. Estimating the dimension of a model. Ann Stat, 6:461–464, 1978.
- Trichopoulos, N. Handanos, J. Danezis, A. Kalandidi, and V. Kalapothaki. Induced abortion and secondary infertility. British Journal of Obstetrics and Gynaecology, 83:645–650, 1976.
- Venables and B. Ripley. Modern Applied Statistics with S. Springer, New York, fourth edition, 2002. URL http://www.stats.ox.ac.uk/ pub/MASS4. ISBN 0-387-95457-0.
- White. Learning in artificial neural networks: a statistical perspective. Neural Computation, 1:425–464, 1989.

Authored by:
Jeffrey Strickland, Ph.D.
Jeffrey Strickland, Ph.D., is the Author of Predictive Analytics Using R and a Senior Analytics Scientist with Clarity Solution Group. He has performed predictive modeling, simulation and analysis for the Department of Defense, NASA, the Missile Defense Agency, and the Financial and Insurance Industries for over 20 years. Jeff is a Certified Modeling and Simulation professional (CMSP) and an Associate Systems Engineering Professional (ASEP). He has published nearly 200 blogs on LinkedIn, is also a frequently invited guest speaker and the author of 20 books including:
- Operations Research using Open-Source Tools
- Discrete Event simulation using ExtendSim
- Crime Analysis and Mapping
- Missile Flight Simulation
- Mathematical Modeling of Warfare and Combat Phenomenon
- Predictive Modeling and Analytics
- Using Math to Defeat the Enemy
- Verification and Validation for Modeling and Simulation
- Simulation Conceptual Modeling
- System Engineering Process and Practices
Connect with Jeffrey Strickland
Contact Jeffrey Strickland
Categories: Articles, Education & Training, Featured, Jeffrey Strickland




Excellent article!
LikeLike
Rare because I couldn’t find many R neural network references. Even though I finished Andrew Ng’s course and have been aware of many other NN resources the bibliography in this article is daunting. Can the author simplify the steps required to gain NN expertise ? I am a IT programmer.
LikeLiked by 1 person
I do not think I can simplify them more using R. However, there are other tools (commercial) with GUI that makes it simpler for a non programmer. Other may know of additional open-source tools.
LikeLike
“A matrix with n rows and three columns will exclude n weights, where the first column indicates the layer, the second column the input neuron of the weight, and the third neuron the output neuron of the weight.”
This should be ? “third column the output neuron of the weight.”
LikeLiked by 1 person
Thanks a lot for your article Jeffrey,
I’m searching for a package in R which implement NARX networks for realtime forecasting, and I would appreciate if someone can bring me some information or bibliografy about it.
LikeLiked by 1 person
Those are the pros, now here are some of the cons:. Firstof all,
before jumping into Ecig comparison, one should know what ane-cigarette is and how it works.
Have the materials lowered to the ground and avoid throwing or dropping
them.
LikeLiked by 1 person
An actual, scientific comparison was not the intent. The data is a from an R dataset that I didn’t have to go out and buy, which is what one world have to do for a real comparison, plus what you rightly suggest in understanding the underlying data. One of the cons of using a neural network is that the algorithm doesn’t care about the underlying data and will learn from it, whether it is right or wrong. I have always argued that analysts must not only understand the underling data, but also the underlying phenomenon. Be that as it may, this was merely a tutorial on using R and nothing more.
LikeLike
Hey, I think your blog might be having browser compatibility issues.
When I look at your blog site in Firefox, it looks fine but when opening in Internet Explorer, it has some
overlapping. I just wanted to give you a quick heads up!
Other then that, great blog!
LikeLike
Really helpful article. I was looking for the default algorithm in neural net. I managed to find it here. Thank you very much. 🙂
LikeLike
Hi really helpful. I am just wondering about interpretation of the Neural network. How could one best summarize the results.
LikeLike